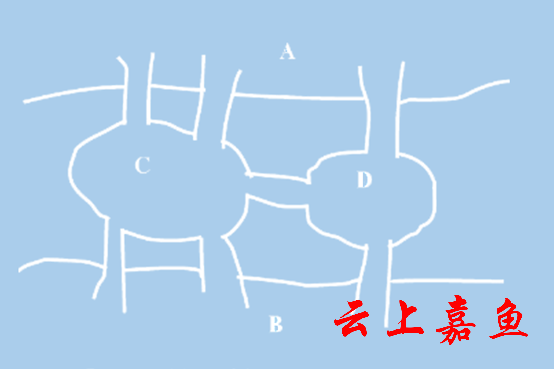
德国哥尼斯堡有一条大河，哥尼斯堡整个城市被这条大河分割成四块区域，而四块区域全靠架在河上的七座桥互相联系。那么一个人能否从某一陆地出发，在不重复每座桥的情况下，回到原来的出发地？这就是历史上有名的哥尼斯堡七桥问题。

这个问题看起来并不难，所以很多人前来尝试，但日复一日，谁也没想出来个所以然。一传十，十传百，七座桥问题很快传遍欧洲，成了欧洲闻名的难题，数学家欧拉知道后，也决心在这个问题上试一试。

欧拉最开始想到的是穷举法，但是这种解法太繁琐了。同时，欧拉认为，如果存在更多的桥时，这种方法就毫无实用价值。

然后，欧拉就想到如果用A、B、C、D四个点表示四块陆地，用两点间的线条代表陆地之间的桥梁，七桥问题就会变成一个抽象图形。现在，要解决的就是否可以“一笔画”这一问题。

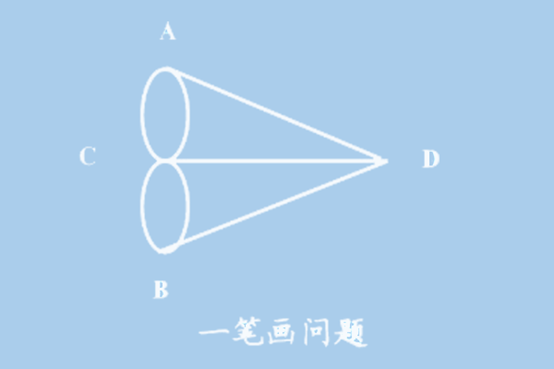
最终，结果证明答案是否定的。除了起点和终点之外，其余的点我们可以称它为中间点。如果要一笔成型，每路过一个中间点，画笔都需要沿另一条线离开这点。一进一出，两两配对，从点发出的线条数肯定会是偶数。因此，我们可以得出决定一笔画成与败的判定规则：一个可以一笔画的图形最多只能有起点和终点这两点与奇数条线相连。

回想欧拉设定的抽象图形，图中的四个点都是与奇数条线相连的，根据判定规则，一笔连通4个点是不会成功的，所以七桥问题所要求的走法也是不成立的。

欧拉解决了七座桥难题，一时之间，欧拉蜚声数坛，但欧拉并没有因此止步，而是不断前进探索数学问题。比如，他证明了当n增加时，数列（1+1/n）n越来越接近（即“趋于”）数字2.71828…。这个数被称为欧拉数或自然常数，简记为e。

今天的故事就讲到这里啦，快去和你的小伙伴分享吧。