1到100中有多少个质数呢？早在公元前250年，古希腊数学家埃拉托色尼，就提出了一种“筛法”，把质数从自然数中筛出来。也就是著名的“埃拉托色尼筛法”。

首先我们来看一下什么是质数。质数就是只能被1和它本身整除的自然数。比方说，5就是质数，因为它只能被1与5这两个数整除。

那埃拉托色尼是怎么把质数筛选出来的呢？我们一起来看一下。

（以100以内的质数的筛选为例）先把1到100这一百个数依次排列。

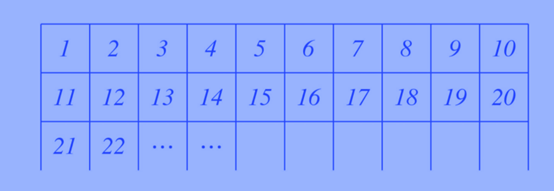
然后把2后面所有2的倍数都划去，凡是2的倍数都是偶数，也就是把2后面的所有偶数划去；再把能被3整除的数（3除外）划掉，接着把能被5整除的数（5除外）划掉……这样一直划下去，最后剩下的数，除1以外都是质数。如：

因此100以内的质数有：2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,61, 67, 71, 73, 79, 83, 89, 97等，共25个。

简而言之，埃拉托色尼筛法是一种通过筛除一个质数所有的倍数，从而识别质数的方法。

现在看来，这个方法很是笨拙，但是“埃拉托色尼筛法”被数学家沿用了两千多年。直到1984年，数学家钱德拉提出了另一种筛法——钱德拉筛法。

钱德拉筛法需要列一个表：

这个表的特点有两个，一是第一行和第一列的数字排法相同；二是，第一行相邻两个数的差是3，第二行相邻两个数的差是5，第三行相邻两个数的差是7，以后以此类推相差9、11、13.....

通过这个表我们可以看出，如果一个自然数N在表中出现，那么2N+1肯定不是质数。比如，4在表中出现，2×4+1=9，9不是质数。

因此通过这个便我们就可以快速的判断这个数是不是质数了，比如103是不是质数呢？

由2N+1=M，可以推出N=（M-1）÷2。

这里M=103，算出N=（103-1）÷2=51。

而51不在表中出现，所以103肯定是质数。

尽管质数是最基本、最重要的数，但是经过几千年的研究，数学家还是没有完全掌握它的规律，期待在未来的某一天，科学家们可以解开这个谜。