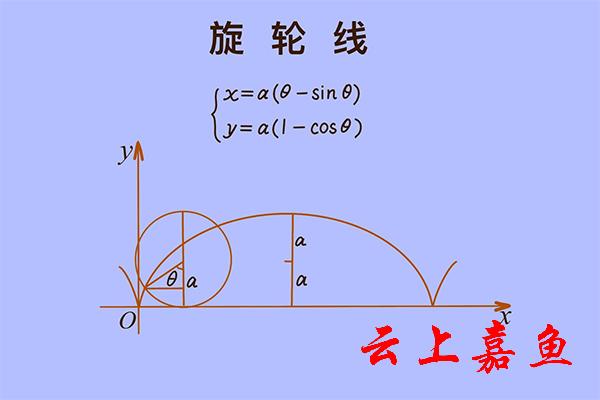
在自行车的轮胎外边缘上用红漆点上一个点，然后让车轮沿直线向前滚动，这个点在空间中所留下来的曲线就是旋轮线。旋轮线也叫摆线，在数学上的定义是一个圆沿着一条直线做无滑动的滚动，圆周上一点画出来的曲线。假如“车轮”不停地转动，画出来的旋轮线也就没有止境。

人们对于旋轮线的研究已久，在17世纪，总结出了它的四个性质：第一，旋轮线的长度等于旋转圆直径的4倍，是一个不依赖于π的有理数；第二，旋轮线在弧线下的面积，是旋转圆面积的三倍；第三，圆上描出旋轮线的那个点，具有不同的速度，在某个特定的地方它甚至是静止的；第四，当弹子从一个摆线形状的容器的不同点放开时，会同时到达底部当中。

旋轮线也叫最速降线，这是因为它具有另一个性质：在忽略摩擦和空气阻力的前提下，当一个物体仅凭重力，从一个点滑落到不在它正下方的另一个点时，如果沿着两点间的旋轮线滑动，所耗费的时间是最短的。这个问题由瑞士数学家约翰・伯努利提出，吸引了许多科学家展开研究，最终牛顿等人得出了沿着旋轮线滚落最省时的结论。

旋轮线在现实生活中应用十分广泛。我国古代宫廷建筑中有一些特殊的屋顶建筑，屋顶从侧面看不是三角形的，而是呈两条曲线，加上屋檐上翘，看起来十分雄壮威严。这种建筑结构就是典型的旋轮线，因为旋轮线的最速降线性质，使得屋顶上的雨水能以最快的速度流走，大大提高了建筑物的安全性。游乐场里跌宕起伏的过山车盘旋轨道，在设计时也利用了旋轮线垂直下降时能达到最高速的性质，使挑战者能感受到最佳的刺激体验。如果你是一个滑板爱好者，应该也知道，在专业的滑板溜碗赛场上，滑出一道最速降线，可以得到最大加速。此外，还有滑梯的蜿蜒滑道，也和旋轮线有着密切的联系。

由此可见，旋轮线既是一条充满速度与激情的运动曲线，又是一条实用性广泛的几何曲线。

本文由中国人民大学附属中学第二分校一级教师秦薇进行科学性把关。

来源：新华网