杨辉三角，又叫做贾宪三角形，帕斯卡三角形。它在中国最早由贾宪在《释锁算术》中提出，后来南宋数学家杨辉在所著的《详解九章算法》中进行了详细说明。

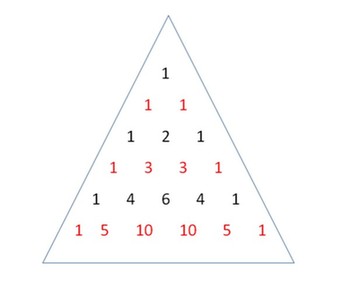
杨辉三角中的三角形数表，是自然界和谐统一的体现。杨辉三角是二项式系数在三角形中的一种几何排列，其中蕴含着二项式系数的几个相关性质，包括二项式系数的对称性、增减性与最大值、各二项式系数的和等。

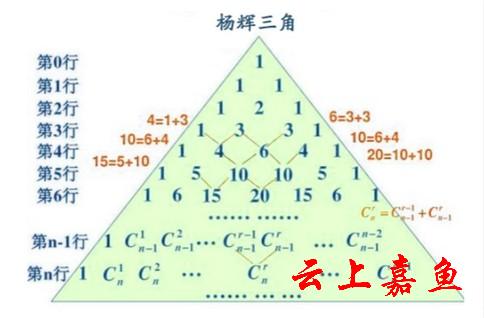
杨辉三角中不只有这些规律，它本身也包含了很多奇妙的性质。杨辉三角的前提是每行数字开头与结尾的数都为1；第n行的数字有n项，且数字之和为2n-1；在第n行中，第m个数与第n-m+1的数值相同，这便是组合数的性质之一；第n行中的第m个数可以表示为：C（n-1，m-1），也就是从n-1个元素当中选取 m-1个元素，这属于杨辉三角的基本性质之一；每个数字与上方两数之和相同，按照此规律便能够得出整个杨辉三角，即第n+1行中第i个数的数值为第n行中第i-1个数与第i个数相加之和，这便是组合数的又一大性质，用公式可以表示为：C（n+1，i）=C（n，i）+C（n，i-1）。

在古老的杨辉三角中存在着很多奥秘，除了数学方面，杨辉三角也与许多诗文形成映射，展现了诗文之美。

一、 杨辉三角的外形与宝塔诗

唐代白居易有一首《一七令·诗》

诗，

绮美，瑰奇。

明月夜，落花时。

能助欢笑，亦伤别离。

调清金石怨，吟苦鬼神悲。

天下只应我爱，世间唯有君知。

自从都尉别苏句，便到司空送白辞。

这种诗体名为宝塔诗，都是宽底尖顶，两侧对称的结构。除第一句外，每行每句相比上一行增加一字。从外形上看，富有美感的宝塔诗和杨辉三角很是相似。

二、 递推链与连环章

杨辉三角每行首尾数字都是1，中间的每个数刚好是该数两肩上的数字之和。这种层层递推的数链结构，表现在文学中就是连环章。

如经典的诗文有《桃话冷落》：“桃花冷落被风飘，飘落残花过小桥。桥下金鱼双戏水，水边小鸟理新毛。毛衣未湿黄梅雨，雨滴江梨分外娇……敲门借问天台路，路过小桥有断桥，桥边种碧桃。”全诗一气呵成，从“桃”字开始，首尾相连，每句首字是上一句末字，顶真回环。句与句之间的关系和杨辉三角行与行之间层层递推的关系有着异曲同工之妙；全诗首尾同字，也和杨辉三角每行首尾都是1结构相同。

杨辉三角虽然是数学问题，但是只要用心观察，便会发现它在很多方面都有着神奇的魅力。